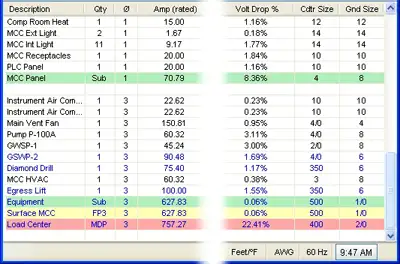
Three Phase Electricity Explained

Three phase electricity delivers power using three alternating currents that are offset in phase. It provides consistent and efficient energy for industrial, commercial, and high-load applications, improving stability and reducing conductor size.

What is Three Phase Electricity?

Three phase electricity is a power system that uses three alternating currents, each offset by 120 degrees, to deliver constant power flow.

✅ Delivers more efficient and stable power than single-phase systems

✅ Ideal for large motors, commercial buildings, and industrial equipment

✅ Reduces conductor material and energy loss over long distances

Three phase voltage, frequency and number of wires

Three phase electricity is the dominant method of electrical power generation, transmission, and distribution across the industrialized world. Unlike single-phase systems, which rely on a single alternating current, three-phase systems use three separate currents, each 120 degrees out of phase with the others. This setup provides a consistent and balanced power flow, making it significantly more efficient for high-demand applications, such as motors, transformers, and large-scale infrastructure. Understanding the difference between alternating current and direct current is essential to grasp how three-phase systems deliver constant power using offset waveforms.

Understanding the Concept

At the heart of a three-phase system are three sinusoidal waveforms, evenly spaced to maintain a continuous flow of energy. When one phase reaches its peak, the others are in different parts of their cycle, ensuring that at any given moment, some power is being delivered. This creates what is known as constant power transfer, a major advantage over single-phase systems that experience power dips between cycles. Since three-phase systems rely heavily on accurate current flow measurement, it’s important to know what ammeters measure and how they help monitor system balance.

For industrial and commercial operations, this stability translates to increased energy efficiency, extended equipment lifespan, and reduced operating costs. Large electric motors, for example, run more smoothly on three-phase power, which avoids the surging and vibration commonly associated with single-phase inputs.

A Brief History

Three phase electricity wasn’t invented by a single person but emerged through the contributions of several pioneers in the late 19th century. Galileo Ferraris in Italy, Nikola Tesla in the United States, and Mikhail Dolivo-Dobrovolsky in Europe all played crucial roles in developing and refining the idea of three-phase alternating current. Tesla’s patents and Dolivo-Dobrovolsky’s practical systems laid the groundwork for what is now a global standard. Engineers use wattmeters to accurately measure real power in three-phase systems, while Watts Law helps calculate the relationships between voltage, current, and power.

Wye and Delta Configurations

Three-phase systems are typically wired in one of two configurations: the Wye (Y) or Delta (Δ) configuration. Each has specific advantages depending on the application:

In a Wye connection, each phase is tied to a central neutral point, allowing for multiple voltage levels within the same system. This is common in both commercial and residential applications, where both high and low voltages are required.
A Delta connection utilizes a closed loop with no neutral, a configuration commonly found in industrial setups. It delivers the same voltage between all phases and is ideal for running large motors without needing a neutral return path.

One of the most important relationships in these configurations is the √3 ratio between line voltage and phase voltage, a fundamental aspect that engineers use in calculating load, cable sizing, and protective device coordination.

Technical Benefits

Three-phase systems have built-in advantages that go beyond stability. Because the sum of the three phase currents is zero in a balanced load, a neutral wire is often unnecessary. This reduces the amount of conductor material needed, lowering costs and simplifying design. Additionally, three-phase motors naturally create a rotating magnetic field, eliminating the need for external circuitry to start or maintain rotation.

Another major benefit is that power output remains consistent. In single-phase systems, power drops to zero twice per cycle, but three-phase systems deliver non-pulsating power, which is especially important in sensitive or precision equipment. The function of a busbar is especially important in three-phase distribution panels, helping to manage multiple circuit connections efficiently.

Where and Why It’s Used

While most homes use single-phase electricity, three-phase is the standard in virtually all commercial and industrial environments. Factories, data centers, hospitals, and office buildings rely on it to power everything from HVAC systems and elevators to conveyor belts and industrial machines.

Three-phase is also common in electric vehicle (EV) charging stations and renewable energy systems, where efficient, high-capacity delivery is essential. If you're working with three-phase motors or transformers, knowing the role of a conductor and how electrical resistance affects current flow is fundamental to efficient design.

For sites that only have access to single-phase power, phase converters—whether rotary or digital—can simulate three-phase conditions, enabling them to operate three-phase equipment. This flexibility has made three-phase solutions accessible even in remote or rural areas. Three-phase systems often operate at medium voltage, especially in commercial settings, and their stability can reduce the risks of ground faults.

EF Partner Media

Video

How Circuit Breaker Monitoring Helps Detect Problems Before Failure Article

Harmonic Distortion Catalog

2024 HVAC catalog Canada Product

OERSTED™

Voltage Levels and Color Codes

Depending on the region, the standard line and phase voltages vary. In North America, typical voltage values include 120/208 volts and 277/480 volts, whereas in Europe and much of Asia, 230/400 volts is more common. Wiring color codes also differ: red/yellow/blue in Europe, black/red/blue in North America, and other variations depending on the country's electrical code. These standards ensure safety, compatibility, and ease of troubleshooting.

The Global Standard for Power

Three-phase electricity is not just a technical solution; it is the foundation of modern electrical infrastructure. Its ability to deliver large amounts of power efficiently, safely, and reliably has made it the system of choice for more than a century. From powering the machines that build our world to the systems that keep us connected, three-phase electricity remains indispensable.

Related News

Harmonic Distortion

Harmonic distortion is the deviation from the ideal electrical waveform caused by nonlinear loads. It impacts power quality, increases heat in equipment, and can lead to system inefficiencies. Monitoring and mitigation are essential in industrial electrical systems.

What is Harmonic Distortion?

Harmonic distortion is not a new phenomenon in power systems. Concern over distortion has fluctuated several times throughout the history of AC electric power systems.

✅ Reduces overall power quality and system reliability

✅ Can damage equipment and increase heat generation

✅ Requires monitoring to ensure system efficiency and safety

In the 1930s and 1940s, the primary sources were transformers, with the primary problem being inductive interference with open-wire telephone systems. Early arc lighting caused similar concern due to its harmonic content, just as today’s electronic power converters do.

Today, nonlinear devices like variable frequency drives (VFDs), arc furnaces, computer power supplies, and LED lighting introduce significant harmonic distortion into electrical systems. Nonlinear devices do not draw current in a linear relationship to voltage, which distorts the sinusoidal waveform and introduces harmonic currents. Harmonic distortion is one of the many issues covered in our comprehensive Power Quality resource channel, which explores causes, effects, and solutions.

Why It Matters

Harmonics degrade power quality
Increase energy losses and heat in conductors and transformers
Lead to premature failure of motors and sensitive electronics
Interfere with communication lines

In contrast, voltage sags and interruptions are nearly universal to every feeder and represent the most numerous and significant power quality deviations. The end-user sector suffers more from harmonic problems than the utility sector. Industrial users with adjustable speed drives, arc furnaces, induction furnaces, and similar equipment are significantly more susceptible to problems caused by harmonic distortion. To understand the relationship between harmonics and apparent energy flow, see our explanation of Apparent Power vs Real Power.

A good assumption for most utilities in the United States is that the sine wave voltage generated in central power stations is very good. In most areas, the voltage found on transmission systems typically has much less than 1% distortion. However, the distortion increases as the load approaches. At some loads, the current waveforms barely resemble a sine wave. Electronic power converters can chop the current into seemingly arbitrary waveforms. Managing nonlinear loads often requires Power Factor Correction to reduce harmonic effects and improve efficiency.

Industry Standards

IEEE 519: Sets recommended harmonic limits for both voltage and current.
IEC 61000-4-7: Defines methods of measuring harmonics and interharmonics.

Harmonic Distortion and Nonlinear Devices

Harmonic distortion is caused by nonlinear devices in the power system. A nonlinear device is one in which the current is not proportional to the applied voltage. Figure 1 illustrates this concept using the case of a sinusoidal voltage applied to a simple nonlinear resistor, where the voltage and current vary according to the curve shown. While the applied voltage is perfectly sinusoidal, the resulting current is distorted. Increasing the voltage by a few percent may cause the current to double and exhibit a different waveform. You can calculate your system’s power quality impact using our Apparent Power Calculator for precise performance metrics.

This is the source of most harmonic distortion in a power system. Figure 1 illustrates that any periodic, distorted waveform can be expressed as a sum of sinusoids. When a waveform is ideal from one cycle to the next, it can be represented as a sum of pure sine waves in which the frequency of each sinusoid is an integer multiple of the fundamental frequency of the distorted wave. This multiple is called a harmonic of the fundamental, hence the name of this subject matter. The sum of sinusoids is referred to as a Fourier series, named after the great mathematician who discovered the concept. Nonlinear loads like VFDs and arc furnaces can affect grounding; learn more in our guide to Electrical Grounding.

Fig. 1. Current distortion caused by nonlinear resistance

Voltage and Current Distortion

The term "harmonics" is often used by itself without further qualification. Generally, it could mean one of the following three:

The harmonic voltages are too great (the voltage is too distorted) for the control to properly determine firing angles.
The harmonic currents are too great for the capacity of some devices in the power supply system, such as transformers, and the machine must be operated at a lower than rated power.
The harmonic voltages are too great because the harmonic currents produced by the device are too great for the given system condition.

Clearly, there are separate causes and effects for voltages and currents, as well as some relationship between them. Thus, the term harmonics by itself is inadequate to describe a problem definitively. Nonlinear loads appear to be sources of harmonic current, injecting harmonic currents into the power system. For nearly all analyses, it is sufficient to treat these harmonic-producing loads simply as current sources. There are exceptions to this as described later.

Fig 2. Harmonic currents flowing through the system impedance result in harmonic voltages at the load.

Voltage distortion is the result of distorted currents passing through the linear, series impedance of the power delivery system, as illustrated in Fig. 2. Although assuming that the source bus is ultimately a pure sinusoid, there is a nonlinear load that draws a distorted current. The harmonic currents passing through the system's impedance cause a voltage drop for each harmonic. This results in voltage harmonics appearing at the load bus. The amount of voltage distortion depends on the impedance and the current. Assuming the load bus distortion stays within reasonable limits (e.g., less than 5%), the amount of harmonic current produced by the load is generally constant.

While the load current harmonics ultimately cause voltage distortion, it is worth noting that the load has no control over the voltage distortion. The same load put in two different locations on the power system will result in two different voltage distortion values. Recognition of this fact is the basis for the division of responsibilities for harmonic control that is found in standards such as IEEE Std 519-1992.

Control over the amount of harmonic current injected into the system occurs at the end-use application.
Assuming the harmonic current injection is within reasonable limits, the control over voltage distortion is exercised by the entity that controls the system impedance, typically the utility.

One must be careful when describing harmonic distortion phenomena, as there are distinct differences between the causes and effects of harmonic voltages and currents. The use of the term harmonics should be qualified accordingly. By popular convention in the power industry, the term is used by itself most of the time when referring to load apparatus, indicating that the speaker is referring to the harmonic currents. When referring to the utility system, the voltages are generally the subject. For systems affected by harmonic-induced overheating, understanding Capacitor Bank applications is essential for voltage support and harmonic filtering. For in-depth harmonic analysis, explore our guide to using a Power Quality Analyzer to identify waveform distortion and power anomalies.

Power Quality Channel

Tidal Electricity From Wave Action

Tidal electricity converts predictable ocean tides into renewable energy using tidal turbines, barrages, and lagoons, delivering stable baseload marine power, efficient grid integration, low carbon emissions, and robust reliability through advanced hydrodynamics and power electronics.

What Is Tidal Electricity?

Tidal electricity generates grid power from ocean tides via turbines or barrages, providing predictable, low-carbon output.

✅ Uses tidal stream turbines, barrages, and lagoons

✅ Predictable output enhances grid stability and capacity planning

✅ Power electronics enable efficient conversion and grid integration

Tidal electricity is obtained by utilizing the recurring rise and fall of coastal waters. Marginal marine basins are enclosed with dams, making it possible to create differences in the water level between the ocean and the basins. The oscillatory flow of water filling or emptying the basins is used to drive hydraulic turbines which propel wave generators. As a specialized branch of hydroelectricity, tidal schemes convert predictable water level differences into dispatchable power.

The cyclical movement of seawater exemplifies how water electricity systems depend on fluid dynamics and site geometry.

Large amounts of wave generation could be developed in the world's coastal regions having tides of sufficient range, although even if fully developed this would amount to only a small percentage of the world's potential hydroelectric power. In global electricity production portfolios, tidal energy typically plays a niche role alongside other renewables.

Because installations are coastal and infrastructure-intensive, they can contribute to regional green electricity targets with long service lives.

It is produced by turbines operated by tidal flow. Many ideas for harnessing the tides were put forward in the first half of the 20th century, but no scheme proved technically and economically feasible until the development by French engineers of the plan for the Rance power plant in the Gulf of Saint-Malo, Brittany, built 1961–67. A dam equipped with reversible turbines (a series of fixed and moving blades, the latter of which are rotated) permits the tidal flow to work in both directions, from the sea to the tidal basin on the flood and on the ebb from the basin to the sea. The Rance plant has 24 power units of 10,000 kilowatts each; about seven-eighths of the power is produced on the more controllable ebb flow. The sluices fill the basin while the tide is coming in and are closed at high tide. Emptying does not begin until the ebb tide has left enough depth of fall to operate the turbines. Conversely, the turbines are worked by the incoming tide to the basin. With reversible bulb turbines, both ebb and flood flows generate electricity with high capacity factors during spring tides.

Compared with windmills for electricity, tidal turbines benefit from dense water flow that yields steadier torque.

The Soviet Union completed construction in 1969 of a plant of about 1,000 kilowatts on the White Sea. Other sites of interest for tidal power plants include the Bay of Fundy in Canada, where the tidal range reaches more than 15 m (49 feet). Although large amounts of power are available from the tides in favourable locations, this power is intermittent and varies with the seasons. Grid planners often pair tidal plants with storage and flexible resources used in electricity windmill operations to smooth variability.

Home Electricity - Electrical Energy Information

Home electricity powers lighting, appliances, and electronics using energy from the grid or renewable sources like solar. Understanding usage, safety, and efficiency helps reduce costs and improve performance in daily life.

What is Home Electricity?

Home electricity refers to the power used to operate household systems and devices.

✅ Powers lights, appliances, HVAC, and electronics

✅ Supplied by utilities or solar energy systems

✅ Measured in kilowatt-hours and billed monthly

How Electricity Enters and Flows Through Your Home

Electricity originates from a distant power station, fueled by coal, natural gas, nuclear power, or renewable sources, and is transformed into high-voltage energy for long-distance transmission. Along the way, transformers step this voltage down to safe, usable levels. When it reaches your home, the electricity flows through a service line to a main panel, where circuit breakers distribute it to branch circuits that power every room and outlet.

In the United States, most residential circuits provide about 120 volts of alternating current (AC) at 60 Hz. Voltage measures the energy per unit charge: 120 volts means 120 joules of energy are transported by each coulomb of charge. One coulomb per second equals one ampere, so an appliance drawing 1 ampere at 120 volts consumes energy at 120 watts—120 joules per second.

How Appliances Use Electrical Energy

When you switch on an appliance, it allows 120 volts of potential to push current through the device—similar to using water pressure to move water through a pipe. As electric charge flows, energy is transformed into useful work like heating, lighting, or mechanical motion. Voltage gradually drops to nearly zero by the time the current exits the appliance.

This “spent” charge is carried back to your electrical panel via the neutral wire and ultimately to the ground through the grounding system. The ground serves as a vast reservoir, stabilizing voltages and protecting users in the event of a fault.

Understanding Home Wiring and Safety

In a standard polarized receptacle, the smaller prong connects to the hot wire (120 volts), and the wider prong to the neutral (0 volts). The hot wire delivers the current; the neutral completes the circuit back to the panel. A separate ground wire exists for safety—it’s not part of the working circuit but protects against electric shock if a fault occurs.

Most wall outlets contain two receptacles (a duplex) wired in parallel. This means two appliances plugged in will receive the same 120-volt supply but can draw different amounts of current. Parallel wiring is standard throughout the home, allowing consistent voltage distribution while accommodating various electrical loads.

Where the Energy Comes From and Where It Goes

Electricity used at home ultimately comes from generators that elevate the voltage of electric charge before it travels across the grid. After powering your home, the now low-energy charge returns to the ground. This closed-loop system—from the earth to the generator and back—enables efficient energy use and the safe disposal of spent charge.

Whether your electricity comes from traditional utilities or rooftop solar panels, the underlying principles remain the same: raise voltage at the source, deliver it efficiently, use it safely, and return it to ground. Understanding these concepts helps homeowners stay informed, reduce waste, and use electricity more safely and effectively.

Electricity and Electrical Energy

Electricity powers modern engineering, driving circuits, voltage, current, and AC/DC power systems for transmission, distribution, and control. Engineers analyze resistance, impedance, and frequency, optimize grids, and integrate renewables with transformers, generators, and smart controls.

What Is Electricity?

Electricity is the flow of charge enabling energy conversion, signal transmission, and power control across circuits.

✅ Quantified by voltage (V), current (A), and power (W)

✅ Governed by Ohm's Law, Kirchhoff's Laws, and Maxwell's equations

✅ Transmitted via grids using AC, transformers, and protection

Electricity is a manufactured product. It is not something you pump out of the ground or mine or collect from the sun or wind. For a clear primer on definitions and units, visit what electricity is to ground these ideas.

Electric power is manufactured from a rotating machine that we call an electrical generator. After it is generated, (manufactured) it is then delivered through copper wires to where it is utilized If you want to see how turbines and alternators convert motion into power, explore the electricity generator to understand key components and operation.

Electricity - most people don't understand what it is. They just turn on the light switch or start the appliance or push the button and something works. It's only when there is no electric power available that we start to consider the importance of it in our daily personal and working lives. A step-by-step explanation of fields, voltage, and current is outlined at how electricity works for readers new to the topic.

But the invention of the machine to generate power is right next to the invention of the printing press in the list of major contributions to the advancement of human civilization. For context on pioneers from Faraday to Tesla, review who invented electricity to connect invention with modern grids.

Without it, we would be burning wood and coal to heat our homes and businesses and using oil and candles to light our way in the dark. That is the way it was for humans civilization for countless centuries. Only since the invention of the electric generator have humans been able to advance in every aspect of modern life. In fact, modern living is defined by electric power. This shift from fuels to electrons is traced in the history of electricity to show how infrastructure reshaped society.

We have assembled a series of pages in our web site to help you to understand the business of electricity - how it works and how it is used. To dive deeper into fundamentals before the business aspects, start with electricity: how it works for a concise technical overview.

We hope that you can use this information to better understand the technology and issues behind the manufacturing of electric power. Further reading on thermal, hydro, and renewable pathways is available at how electricity is generated to see how manufacturing methods compare.

Understanding Ground Electricity

Ground electricity underpins grounding and earthing practices, managing earth potential and fault current. It ensures equipotential bonding, surge protection, and safety compliance per IEC/NEC standards for power systems, electronics, and lightning protection.

What Is Ground Electricity?

Ground electricity is the earth reference and return path that stabilizes systems and safely carries fault current.

✅ Provides low-impedance fault current paths to trip protection

✅ Uses earth electrodes, bonding, and grounding conductors

✅ Reduces touch voltage, EMI, and lightning surge damage

Understanding Ground Electricity

Ground Electricity is a general term that is often used loosely to refer to “Bonding” (Safety Grounding) and “Earth Grounding”. Personnel of major industries have often misinterpreted grounding to mean that anything in contact with the earth is considered to be grounded. For foundational context, see our overview on how electricity works to understand why grounding concepts are sometimes conflated.

Electrical Grounding is the reference zero for the electrical system. When we talk about 120 Volts RMS, it represents 120 units above the zero electrical reference. In residential settings, this reference is commonly tied to service equipment, as explained in our guide to home electricity and typical distribution practices.

Electrical Grounding is the reference zero for the electrical system and all the equipment should be at this same equipment potential plane. Maintaining that equipotential plane is central to electricity safety because it minimizes touch voltage hazards.

According to accident reports, most electrical accidents occur when the earth is used as the safety grounding system (Bonding). These incidents underscore the broader dangers of electricity when protective paths are improperly designed.

Accident reports details the hazards of using earth as a safety grounding and the practice of electrical grounding the equipment through local grounds. (grounding each individual piece of equipment with a separate ground rod, driven into the earth). Improper local grounds can also complicate fault clearing during a system electrical fault, increasing damage and downtime.

The best method for ensuring the safety of personnel is to use a “Bonding Conductor”. This conductor should be continuous, with sufficient ampacity and the lowest impedance path back to the circuit interrupting devices, which insures positive operation of the protective devices. A robust bonding network ensures rapid clearing of a ground fault by providing a low-impedance return path for protective devices.

Once a system that connects all the metallic frames of electrical equipment together has been established, then the grounding system must be placed at “Zero Reference Potential”. The earth grounding electrode should have the lowest resistance value possible, preferably 5 ohms or less. Coordinating equipment bonding with proper transformer grounding helps maintain stable reference potential across the installation.

This low resistance to earth ground electricity will limit the potential of the electrical system to earth (limiting the stresses placed on components such as switches, insulators and transformers).

It will also reduce the effects of static charges on the electrical system and will protect against lightning strokes, lightning induced voltages, and minimizes the effects of transient over-voltages.

Visit Our Electrical Grounding and Bonding Course

Electricity Power Explained

Electricity power underpins voltage, current, and wattage in generation, transmission, and distribution across the grid, integrating AC/DC systems, transformers, generators, load management, power factor correction, and renewable energy for efficient, reliable supply.

What Is Electricity Power?

Electricity power is energy transfer rate: voltage times current, yielding watts in AC/DC systems.

✅ P = V * I; apparent, real, reactive power relationships

✅ Power factor improves efficiency and reduces I^2R losses

✅ Transformers step voltage for transmission efficiency

The make up of the electricity power sector has been in transition over recent history. In most provinces, there has been a transition from traditional electric utilities (which are mostly provincially-owned crown corporations) to private generation, transmission and distribution assets. For context, industry overviews such as electricity generation in Canada outline how policy and market structures influence capacity additions today.

In 2014, Canadian eutilities and industrials generators produced more than 639 terawatt hours of electricity. When it comes to hydroelectric power, Canada is the world's second largest producer. Hydroelectricity accounts for 59.3 per cent of Canada’s supply. Other energy sources that contribute to the transfer of energy include: coal, uranium, natural gas, petroleum and non-hydro renewable energy sources. About 67 per cent of Canada’s energy comes from renewable sources like wind, solar and hydroelectric power stations and 82% from non-greenhouse gas emitting sources. A breakdown of major fuels is available through sources of electricity for readers comparing provincial mixes.

Hydropower output is intrinsically linked to water availability and operations, and resources on water and electricity explain how hydrology and infrastructure shape generation profiles.

In 2014, almost 59 terawatt hours of electricity exported to the USA, while about 13 terawatt hours was imported from the United States. These trade patterns reflect how provinces balance load and generation portfolios, as noted in discussions of electricity supply dynamics under varying market conditions.

Canada's industrial sector is responsible for the largest share of electricity demand because there are a number of energy-intensive industrial activities like mining, oil and gas production, pulp and paper production, and other primary industry uses. Residential and commercial sectors consume much smaller quantities of electricity for lighting (light bulb), heating, and communications. Detailed consumption patterns can be explored in Canada's electricity demand by sector and region.

R&D programs aimed at maintaining the operating capability of the nation’s existing nuclear power plants and developing the next generation of nuclear technologies. Nuclear energy is the world’s largest source of emission-free electricity power. The Nuclear Energy program is working to develop cost-efficient technologies that further enhance nuclear safety, minimize the generation of nuclear waste, and further reduce the risk of proliferation. Within the broader generation portfolio, resources like nuclear are profiled in guides on how electricity is generated across different technologies.

To meet the rising demand of the 21st century, significant improvements in America’s electric system are necessary. Blackouts serve as a powerful reminder of the critical role electricity plays in the everyday lives of people.

Voltages, currents, power energy

When it comes to electric current, electrical voltage, electric circuit dynamics and energy powers, all rely on the flow of the electron. What this means is that power voltage feeds loads, solid state power load devices, and other loads that need electric power. Electric power is the rate at which that power is measured in watts or voltage in volts. There are various forms of energy measured in si unit: apparent power, reactive power, ac power, real power in watts, etc. For a refresher on fundamental concepts and terminology, see what is electricity to connect these quantities with practical applications.

Electrical Engineers and Scientists alike seek common views in order to develop new technologies for the storage of energy and the transmission of electric potential through power circuits that will contribute to energy efficiency of the electric industry. For instance, the copper wires used in typical transmission lines lose a percentage of the electricity passing through them because of resistance over long distances, which causes the wires to heat up. But "superconducting" materials have no resistance, and if they are used to transmit electricity in the future, very little of the electricity will be lost.

Electricity Today T&D Magazine Subscribe for FREE

Stay informed with the latest T&D policies and technologies.

Timely insights from industry experts
Practical solutions T&D engineers
Free access to every issue

Download the 2026 Electrical Training Catalog

Download the 2026 Electrical Training Catalog

Three Phase Electricity Explained