Voltage Drop Formula
The voltage drop formula is V = I × R, where V represents the voltage drop, I represents the current in amperes, and R represents the resistance in ohms. It calculates the amount of voltage lost through a conductor and is essential for designing safe and efficient electrical systems.
What is Voltage Drop Formula?
A voltage drop formula can help you manually calculate the voltage drop in cables under full load in branch circuits. It does not matter if you are working with copper or aluminum conductors. To accurately calculate the voltage drop for a given cable size, length, and current, you need to know the resistance of the type of cable you’re using.
✅ V = I × R for DC circuits
✅ Accounts for impedance in AC circuits
✅ Helps ensure safe, efficient electrical design
Use our voltage drop calculator to quickly determine wire size, conductor efficiency, and line loss for safer, more reliable electrical installations.
Power Quality Analysis Training
Request a Free Power Quality Training Quotation
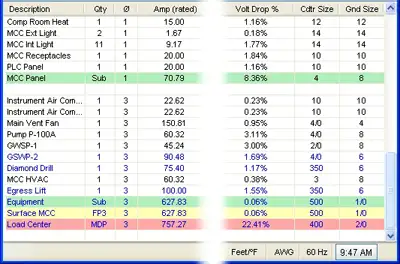
To determine voltage drop in an electrical system, engineers and electricians use a standard formula that accounts for conductor resistance, current, and circuit length. The National Electrical Code (NEC) provides guidelines for the maximum voltage drop allowed in various installations to ensure efficiency and safety. For both single-phase and three-phase circuits, excessive voltage drop can lead to poor equipment performance and energy loss. To simplify calculations, a voltage drop calculator can quickly assess whether a circuit meets NEC recommendations and optimize conductor sizing accordingly. You can learn more about how electrical resistance affects circuits in our detailed voltage drop guide, which explains causes, calculations, and solutions for safe, efficient power distribution.
DC / single phase calculation
The voltage drop V in volts (V) is equal to the wire current I in amps (A) times 2 times one way wire size length L in feet (ft) times the wire resistance per 1000 feet R in ohms (Ω/kft) divided by 1000:
Vdrop (V) = Iwire (A) × Rwire(Ω)
= Iwire (A) × (2 × L(ft) × Rwire(Ω/kft) / 1000(ft/kft))
The voltage drop V in volts (V) is equal to the wire current I in amps (A) times 2 times one way wire length L in meters (m) times the wire resistance per 1000 meters R in ohms (Ω/km) divided by 1000:
Vdrop (V) = Iwire (A) × Rwire(Ω)
= Iwire (A) × (2 × L(m) × Rwire (Ω/km) / 1000(m/km))
3 phase calculation
The line-to-line voltage drop V in volts (V) is equal to the square root of 3 times the wire current I in amps (A) times one-way wire length L in feet (ft) times the wire resistance per 1000 feet R in ohms (Ω/kft) divided by 1000:
Vdrop (V) = √3 × Iwire (A) × Rwire (Ω)
= 1.732 × Iwire (A) × (L(ft) × Rwire (Ω/kft) / 1000(ft/kft))
The line-to-line voltage drop V in volts (V) is equal to the square root of 3 times the wire current I in amps (A) times one-way wire length L in meters (m) times the wire resistance per 1000 meters R in ohms (Ω/km) divided by 1000:
Vdrop (V) = √3 × Iwire (A) × Rwire (Ω)
= 1.732 × Iwire (A) × (L(m) × Rwire (Ω/km) / 1000(m/km))
Wire diameter calculations
The n gauge wire diameter, dn in inches (in), is equal to 0.005in times 92 raised to the power of 36 minus gauge number n, divided by 39:
dn (in) = 0.005 in × 92(36-n)/39
The n gauge wire diameter dn in millimetres (mm) is equal to 0.127mm times 92 raised to the power of 36 minus gauge number n, divided by 39:
dn (mm) = 0.127 mm × 92(36-n)/39
Wire cross-sectional area calculations
The n gauge wire's cross-sectional area An in kilo-circular mils (kcmil) is equal to 1000 times the square wire diameter d in inches (in):
An (kcmil) = 1000×dn2 = 0.025 in2 × 92(36-n)/19.5
The n gauge wire's cross-sectional area An in square inches (in2), is equal to pi divided by 4 times the square wire diameter d in inches (in):
An (in2) = (π/4)×dn2 = 0.000019635 in2 × 92(36-n)/19.5
The n gauge wire's cross-sectional area, An, in square millimetres (mm2), is equal to pi divided by 4 times the square wire diameter d in millimetres (mm):
An (mm2) = (π/4)×dn2 = 0.012668 mm2 × 92(36-n)/19.5
Wire resistance calculations
The n gauge wire resistance R in ohms per kilofeet (Ω/kft) is equal to 0.3048×1000000000 times the wire's resistivity ρ in ohm-meters (Ω·m) divided by 25.42 times the cross-sectional area An in square inches (in2):
Rn (Ω/kft) = 0.3048 × 109 × ρ(Ω·m) / (25.42 × An (in2))
The n gauge wire resistance R in ohms per kilometre (Ω/km) is equal to 1000000000 times the wire's resistivity ρ in ohm-meters (Ω·m) divided by the cross-sectional area An in square millimetres (mm2):
Rn (Ω/km) = 109 × ρ(Ω·m) / An (mm2)
Related Pages