What is a Watt? Electricity Explained
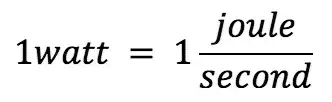
A watt is the standard unit of power in the International System of Units (SI). It measures the rate of energy transfer, equal to one joule per second. Watts are commonly used to quantify electrical power in devices, circuits, and appliances.
What is a Watt?
A watt is a unit that measures how much power is used or produced in a system. It is central to understanding electricity and energy consumption.
✅ Measures the rate of energy transfer (1 joule per second)
✅ Commonly used in electrical systems and appliances
✅ Helps calculate power usage, efficiency, and energy costs
A watt is a unit of power, named after engineer James Watt, which measures the rate of energy transfer. A watt is a unit of power that measures the rate at which energy flows or is consumed. One watt is equivalent to one joule per second. In terms of electrical usage, 1,000 watt hours represent the amount of energy consumed by a device using 1,000 watts over one hour. This concept is important for understanding power consumption across devices on the electric grid. The watt symbol (W) is commonly used in electricity to quantify power, and watts measure power in various contexts, helping to track energy flow efficiently.
Frequently Asked Questions
How does a watt relate to energy?
A watt is a unit of power that measures the rate at which energy is consumed or produced. Specifically, one watt equals one joule per second, making it a crucial unit in understanding how energy flows.
How is a watt different from a watt-hour?
A watt measures power, while a watt-hour measures energy used over time. For instance, if you use a 100-watt bulb for 10 hours, you've consumed 1,000 watt-hours of energy.
How many watts does a typical household appliance use?
Wattage varies between appliances. For example, a microwave uses 800 to 1,500 watts, while a laptop typically uses between 50 to 100 watts. Understanding the wattage helps estimate overall power consumption.
What does it mean when a device is rated in watts?
A device’s watt rating indicates its power consumption when in use. A higher wattage means the device draws more power, leading to higher energy costs if used frequently.
How can I calculate power consumption in watts?
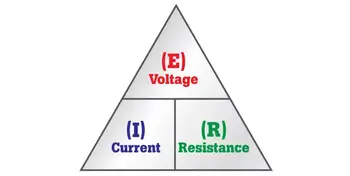
To calculate power in watts, multiply the voltage (volts) by the current (amperes). For example, a device using 120 volts and 10 amps will consume 1,200 watts. A watt, in electrical terms, is the rate at which electrical work is done when one ampere (A) of current flows through one volt (V). Formula:
W= A* V
Whenever current flows through a resistance, heat results. This is inevitable. The heat can be measured in watts, abbreviated W, and represents electrical power. Power can be manifested in many other ways, such as in the form of mechanical motion, or radio waves, or visible light, or noise. In fact, there are dozens of different ways that power can be dissipated. But heat is always present, in addition to any other form of power in an electrical or electronic device. This is because no equipment is 100-percent efficient. Some power always goes to waste, and this waste is almost all in the form of heat.
There is a certain voltage across the resistor, not specifically given in the diagram. There's also electricity flowing through the resistance, not quantified in the diagram, either. Suppose we call the voltage E and the current I, in volts and amperes, respectively. Then the power in watts dissipated by the resistance, call it P, is the product E X I. That is:
P (watts) = El
This power might all be heat. Or it might exist in several forms, such as heat, light and infrared. This would be the state of affairs if the resistor were an incandescent light bulb, for example. If it were a motor, some of the power would exist in the form of mechanical work.
If the voltage across the resistance is caused by two flashlight cells in series, giving 3 V, and if the current through the resistance (a light bulb, perhaps) is 0.1 A, then E = 3 and I = 0.1, and we can calculate the power P, in watts, as:
P (watts) = El = 3 X 0.1 = 0.3 W
Suppose the voltage is 117 V, and the current is 855 mA. To calculate the power, we must convert the current into amperes; 855 mA = 855/1000 = 0.855 A. Then we have:
P (watts) = 117 X 0.855 = 100 W
You will often hear about milliwatts (mW), microwatts (uW), kilowatts (kW) and megawatts (MW). You should, by now, be able to tell from the prefixes what these units represent. But in case you haven't gotten the idea yet, you can refer to Table 2- 2. This table gives the most commonly used prefix multipliers in electricity and electronics, and the fractions that; they represent. Thus, 1 mW = 0.001 W; 1 uW = 0.001 mW = 0.000001 W; 1 kW = 1-flOO W; and 1 MW = 1,000 kW = 1,000, 000 W.
Sometimes you need to use the power equation to find currents or voltages. Then you should use I = P/E to find current, or E = P/I to find power. It's easiest to remember that P = El (watts equal volt-amperes), and derive the other equations from this by dividing through either by E (to get I) or by I (to get E).
A utility bill is measured in kilowatt hours, usually in 1,000 watt increments. A watt is a unit of electrical energy in which the units of measurement (watts and watt hours) are agreed to by an international system of units si called watts. The amout of energy is measured this way.
Related Articles