Mastering The Three-Phase Power Calculation

Three-phase power is vital to many industrial and commercial applications due to its efficiency and ability to handle high loads. Calculating three-phase power requires considering various factors, including voltage, current, and power factor. The type of connection being used and the power triangle and power factor are also important considerations in three-phase power calculations. Understanding the basics of three-phase power calculation can help ensure the efficient and effective use of electrical power in a variety of applications.

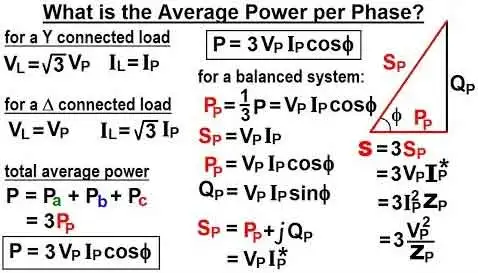
To calculate the total power of a three-phase system, the formula used is as follows:

Total Power (W) = √3 × Voltage (V) × Current (A) × Power Factor

This formula considers that the three-phase system has three separate phases, each with its own voltage and current. Therefore, the square root of three (√3) is a factor that is included to account for the relationship between the line-to-line voltage and the line-to-neutral voltage in a three-phase system.

To calculate the power in each phase of a three-phase system, the formula used is as follows:

Phase Power (W) = Voltage (V) × Current (A) × Power Factor

This formula is similar to the formula for calculating the total power of a three-phase system but only considers the voltage and current in one phase.

There are two main types of three-phase connections: delta and star (also known as wye). In a delta connection, the three-phase power supply is connected in a triangle configuration, with each phase connected to the next. Each phase is connected to a central neutral point in a star connection, creating a Y-shaped configuration. The type of connection being used can affect the voltage and current in the system and should be taken into account when calculating three-phase power.

The power triangle is a visual representation of the relationship between different types of power in a three-phase system. The power triangle is made up of three sides: the real power, reactive power, and apparent power. Real power is the power that is used to perform useful work, while reactive power is the power that is required to create and maintain magnetic fields. Finally, apparent power is the combination of both real and reactive power.

The power factor is also an important consideration in three-phase power calculation. The power factor is a measure of how efficiently the system uses power. A low power factor can lead to inefficiencies in the system and increased energy costs. To calculate the power factor in a three-phase system, the formula used is as follows:

Power Factor = Real Power (W) ÷ Apparent Power (VA)

The line-to-line voltage and line-to-neutral voltage in a three-phase system can also be calculated using the following formulas:

Line-to-Line Voltage (V) = √3 × Line-to-Neutral Voltage (V)

Line-to-Neutral Voltage (V) = Line-to-Line Voltage (V) ÷ √3

The total current can be divided by the square root of three to calculate the amps per phase in a three-phase system. This is because the current in each phase is lower than the total current in a three-phase system. The formula used to calculate amps per phase is:

Amps per Phase (A) = Total

The total current can be divided by the square root of three to calculate the amps per phase in a three-phase system. This is because the current in each phase is lower than the total current in a three-phase system. The formula used to calculate amps per phase is:

Amps per Phase (A) = Total Current (A) ÷ √3

Another important calculation in three-phase power is the conversion of kilowatts (kW) to amps. This can be done using the formula:

Amps (A) = (kW x 1000) ÷ (√3 x Voltage (V))

This formula considers that in a three-phase system, the voltage is measured between phases, while in a single-phase system, the voltage is measured between a phase and neutral.

In a three-phase system, the power factor is typically represented by the symbol cos φ. This value measures the phase angle between the voltage and current in the system. A high power factor indicates that the voltage and current are in phase with one another, while a low power factor indicates that they are out of phase.

How do you calculate power in 3 phase supply?
To calculate power in a three-phase system, use the formula:

Total Power (W) = √3 × Voltage (V) × Current (A) × Power Factor

Why do we calculate 1.73 for 3-phase power?

We calculate 1.73 (the square root of 3) for three-phase power because the voltage measured in a three-phase system is line-to-line, whereas, in a single-phase system, it is line-to-neutral. Therefore, the total voltage across a three-phase system is higher than that across a single-phase system.

How do you calculate 3-phase voltage?

The line-to-neutral voltage in a three-phase system can be found by dividing the line-to-line voltage by the square root of three. This is because the line-to-line voltage is higher in a three-phase system than the line-to-neutral voltage.

How do you calculate amps per phase in a 3-phase system?

To calculate amps per phase in a three-phase system, divide the total current by the square root of three. This is because the current in each phase is lower than the total current in a three-phase system. The formula used to calculate amps per phase is:

Amps per Phase (A) = Total Current (A) ÷ √3

What is three-phase power, and how is it different from single-phase power?

Three-phase power is a type of electrical power made up of three alternating currents 120 degrees out of phase with one another. This allows for more efficient use of power, as the power flow is continuous and more stable than in a single-phase system composed of only one alternating current.

How do you calculate the total power of a three-phase system?

To calculate the total power of a three-phase system, use the formula:

Total Power (W) = √3 × Voltage (V) × Current (A) × Power Factor

How do you calculate the power in each phase of a three-phase system?

To calculate the power in each phase of a three-phase system, use the formula:

Phase Power (W) = Voltage (V) × Current (A) × Power Factor

What is a power factor, and how does it affect three-phase power calculations?

The power factor is a measure of how efficiently the system uses power. In an ideal system, the power factor would be 1, indicating that all of the power being used is being put to productive use. However, in practice, the power factor can be affected by several factors, such as inductive loads and reactive power. Therefore, power factor is an important consideration in three-phase power calculations, as it affects the system's efficiency and can lead to increased energy costs.

What is the difference between active, reactive, and apparent power in three-phase systems?

Active power is the power that is actually used to perform useful work, while reactive power is the power that is required to create and maintain magnetic fields. Finally, apparent power is the combination of both real and reactive power. Understanding the relationship between active, reactive, and apparent power is important in three-phase power calculations, as it can help identify inefficiency in the system.

What is a power triangle, and how is it used in three-phase power calculations?

The power triangle is a visual representation of the relationship between different types of power in a three-phase system. The power triangle is made up of three sides: the real power, reactive power, and apparent power. Real power is the power that is actually used to perform useful work, while reactive power is the power that is required to create and maintain magnetic fields. Apparent power is the combination of both real and reactive power. The power triangle can be used to calculate the power factor and identify areas of inefficiency in the system.

How do you calculate the line-to-line voltage and line-to-neutral voltage in a three-phase system?

The line-to-line voltage in a three-phase system is calculated by multiplying the line-to-neutral voltage by the square root of three. Likewise, the line-to-neutral voltage can be calculated by dividing the line-to-line voltage by the square root of three. These calculations consider that the voltage measured in a three-phase system is line-to-line, whereas it is line-to-neutral in a single-phase system.

Calculating three-phase power requires taking into account various factors, such as voltage, current, and power factor. The 3-phase power formula is the key to understanding the relationship between these factors. By using this formula, you can determine the total power in a three-phase system, as well as the power in each individual phase.

Additionally, converting kW to amps is an essential calculation for three-phase power, as it helps determine the load that a particular system can handle. Understanding the power factor is also critical for three-phase power, as it can have a significant impact on system efficiency. With the right knowledge of phase power equations, you can ensure that your three-phase system is running optimally and safely.