Transformer Losses Explained

Transformer Losses

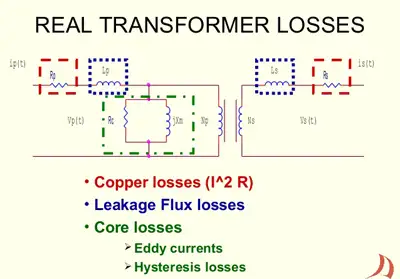
Since distribution transformers has no rotating parts, it has no mechanical losses. This contributes to its high operating efficiency of over 90%. However, like any electrical device, a transformer does have load losses due to several factors. These losses appear in the form of heat and produce an increase in temperature and a drop in efficiency. Losses can be classified into two categories: copper losses and core losses.

Copper Loss: This loss is caused by the resistance of the copper wire in the primary and secondary windings. A transformer winding can consist of hundreds of turns of fine copper wire, resulting in a relatively-high resistance value. As current flows through this resistance, some power is dissipated in the form of heat. Copper losses are minimized by employing large diameter conductors to reduce the resistance per unit length of the wires. Copper losses are generally about twice as great as core losses in most transformers.

Eddy Current Losses: Eddy currents are caused by the alternating current inducing a current in the core of the transformer. The eddy current losses are kept to a minimum though the use of laminated cores. Eddy currents increase with frequency; they are directly proportional to the square of the AC frequency.

Hysteresis Loss

A rather esoteric form of loss, called hysteresis loss, occurs in all ferromagnetic transformer cores, but especially in laminated iron. Hysteresis is the tendency for a core material to act "sluggish" in accepting a fluctuating magnetic field. Air cores essentially never exhibit this type of loss. In fact, air has lowest overall loss of any known transformer core material. Laminated cores exhibit high hysss loss above the AF range, so they don't work well above a few kilohertz.

At frequencies up to several tens of megahertz, powdered iron can serve as an efficient RF transformer core material. It has high magnetic permeability and concentrates the alternating magnetizing flux considerably. High permeability cores minimize the number of turns needed in the coils, thereby minimizing the ohmic (resistive) loss that can take place in the wires.

At the highest radio frequencies (more than a couple of hundred megahertz), air represents the overall choice as a transformer core material because of its low loss and low permeability.

Hysteresis loss occurs in the core and is a result of molecular friction, which is caused by changes in the polarity of the applied current. When the magnetic field reverses, the molecular magnets also reverse their alignment and, in doing so, some power is dissipated in the form of heat.

Leakage Flux: This relatively small loss is the result of the leakage of the electromagnetic flux lines between the primary and secondary winding.

Saturation: Saturation losses may occur if the transformer is loaded beyond its rated capacity. This happens when the core reaches its saturation point and an increase in current produces no additional flux lines.

An ideal transformer would have no heat losses and would therefore be 100% efficient. Transformer efficiency is a function of a transformer's copper and core losses and has nothing to do with power factor. These losses are all measured in watts. The efficiency of a transformer is determined the same way you calculate efficiency for other equipment. Divide the output power by the input power:

Transformers rank among the most efficient of electrical apparatus. In a standard power transformer the full-load efficiency is generally from 96% to 99%. The core losses are approximately constant from no-load to full-load. However, the copper losses vary with the square of the current in the winding and the winding resistance. The no-load efficiency of a transformer is lower than its full-load efficiency. Therefore sizing power transformers to meet their expected loading greatly influences transformer efficiency. Oversized transformers can contribute to inefficiency, but when transformers are appropriately matched to their loads, efficiency increases.

At times line voltages may be either higher or lower than the rated voltage of a transformer's primary. If a transformer has lower-than-rated voltage applied, the kVA is reduced by the same percentage as the voltage is reduced. One or two percent voltage overage will generally be tolerated by most transformers without reduction in M. If the voltage is increased sufficiently above the rated nameplate value, the windings heat excessively and the flux density of the core will increase causing the saturation of the core to be above normal.

Voltage regulation is the measure of how well a power transformer can maintain constant secondary voltage given a constant primary voltage and wide variance in load current. Voltage regulation in transformers is the difference between the no-load voltage and the full-load voltage:

This is usually expressed in the terms of a percentage of the full-load voltage: for example, with a transformer that delivers 100 volts at no-load and 95 volts at full-load, the regulation would be 5%. Transformer voltage regulation depends on the impedance of the load and the total copper loss of the transformer. When supplying a noninductive load, the copper loss contributes to the major portion of the voltage drop. Power and lighting transformers generally have regulation from 2% to 4% depending on the size and application for which they are used.

It is important that a transformer be operated on an AC circuit with frequency for which it is designed. Transformers below 2 kVA are usually designed and rated to be used at 50 or 60 Hz. When a lower frequency what the transformer is designed for is used, the reactance of the primary winding will decrease, resulting in a marked increase in the exciting rent. This increases the flux density in the core and without special desi higher losses and greater heat rise will result. A 60 Hz only transformer design is physically smaller than a 50 Hz design and should not be used on a 50 Hz circuit.

If the frequency is greater than nameplate frequency, there will be an increase in reactance and a decrease in exciting current. There will be, of course, a lower flux density but the core loss will remain practically constant. Operating 60 Hz transformers at higher frequencies may simply provide less voltage regulation.